
Linear momentum
Linear momentum (not to be confused with angular momentum) is a vector quantity that represents an object’s mass, as well as its magnitude and direction of motion. As such, you can think of linear momentum as a measurement of an object’s “mass in motion”.
Mathematically, linear momentum is the product of the mass and velocity of an object. The units for momentum would thus be the units for mass (kg) multiplied by that of velocity (m/s). In physics, linear momentum is often represented by the symbol “p”. The basic formula for momentum can thus be presented like so:
- Formula: Momentum = mass x velocity
- Simplified formula: p = m x v
- SI Units: kg•m/s
Do note that mass and velocity affect the magnitude of linear momentum in equal measure. An increase in either mass or velocity would result in a directly proportionate increase in momentum. To put it simply, if you were to double the mass or velocity of an object, momentum would double as well. However, if velocity is zero, such as when an object is at a complete standstill, the momentum would be zero, regardless of the mass.
Still, just describing an object’s momentum in terms of kg•m/s is insufficient. You may recall that a vector quantity must give information about direction as well. Consider a 20 kg cart rolling westward along a track at a constant speed of 5 m/s. In this case, the direction of the velocity vector is the same as the direction in which the object is moving. Therefore, the velocity would be 5 m/s, west. You would then describe the momentum of the cart as 20 kg x 5 m/s = 100 kg•m/s, west. As you can see, it is crucial to include the direction of momentum.
Conservation of Momentum
The principle of conservation of momentum, more specifically the law of conservation of linear momentum, states that the total momentum of an isolated system remains constant. This means that in the absence of any external forces, the total momentum of a system will not change. This applies to all systems, from individual collisions between two objects to complex interactions between a group of particles.
This concept can also be understood in the context of Newton’s third law. The law states that the forces between two colliding particles are equal in magnitude and opposite in direction. This suggests that the change in force between the two particles will always add up to zero. To describe it as a formula, taking m1 & m2 to be the mass of the two objects, u1 & u2 to be the initial velocity of each object before collision, and v1 & v2 to be the final velocity of each object after collision:
- m1u1 + m2u2 = m1v1 + m2v2
Let’s look at an example to illustrate this concept. Consider two balls, ball 1 and ball 2, rolling towards one another in opposite directions. Suppose that ball 1 has a momentum of 100 kg•m/s, and that object 2 has a momentum of 30kg•m/s. If these two objects were to collide, this would be the result:
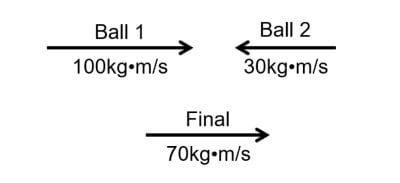
In this case, both balls would move in the initial direction of ball 1 (the ball with the higher velocity) as a single unit, at a momentum of 100 – 30 = 70 kg•m/s. Note that total momentum has not changed. If we take the direction of ball 1 to be the “positive” direction when considering velocity, the initial total momentum was actually 100 – 30 = 70 kg•m/s as well.

In the case of ball 2 being stationary, both balls will simply travel in the direction of ball 1 at the initial momentum of ball 1. It is important to note that this does not mean that both balls travel at the initial velocity of ball 1. Nor does it mean that the momentum of each object stays the same.
| Object | Weight (kg) | Velocity (m/s) | Momentum (kg•m/s) | |
| Before collision | Ball 1 | 5 | 20 | 100 |
| Ball 2 | 15 | 0 | 0 | |
| After collision | Final | 20 | 100/20 = 5 | 100 |
| Ball 1 | 5 | 5 | 5 x 5 = 25 | |
| Ball 2 | 15 | 5 | 15 x 5 = 75 |
As the table above shows, the total momentum of the system still remains constant. However, the velocity and momentum of each object change after the collision. This is the principle of conservation of momentum at work.
The formulae regarding linear momentum and the principle of conservation of momentum are fairly straightforward, but they can be difficult to grasp for a start. Its application can be particularly challenging, especially for those who are not used to dealing with this topic. If you are looking for help to ace your O Levels and A Levels, Best Physics Tuition can aid in your understanding of even the toughest concepts with their engaging and effective physics tuition curriculum.

